Over the next few posts, I'll be writing a series on how chess engines work. This isn't intended to be an authoritative, in-depth guide on engines, but just a quick summary on the different types of chess engines, and how they compare against each other.
History of Chess Engines
Chess is one of the oldest domains of AI research. People have been interested in chess-playing machines since at least the Mechanical Turk. The first serious attempts at building such a machine happened in the 1950s and 60s, when digital computers first became used. While some novel algorithms like the alpha-beta search were developed during this time, chess engines were still extremely weak, mainly due to a lack of processing power.
In the 70s and 80s, processing power grew to such an extent that engines were now able to play at the master level, and eventually were able to score wins at even the GM level. In the 90s, IBM built a supercomputer called Deep Blue which challenged Garry Kasparov. While Kasparov was successful in the 1996 match, Deep Blue won the match in 1997 - marking the first time that a computer defeated a reigning World Champion, and ushering in the era of computer chess dominance.
Minimax
The basic algorithm that chess engines follow is called Minimax. Essentially, the engine will play out all of the possible moves that could arise from the future state, and then work backwards to pick which move results in the best position. The catch is that every other turn, the opponent will also be trying to make the best moves, so it ends up being a two-step process.
If we are working backwards and it's our turn, we would select the best move that we can make. However, when it's our opponent's turn, we want to choose the position in such a way that their best move has the worst outcome (for them).
That was quite an unwieldy explanation, so it might be better to look at some examples.

Here, we can see how this process works. Each of the even steps take place on our turn, and the odd steps take place on our opponent's turn. At the end of the tree, we select the moves with the highest score (since we are trying to get the highest value), and propagate that upwards. Then, we select the move with the lowest score (since our opponent is trying to get the lowest value possible), and propagate that. We continue this process until we get to the top. Once we've finished, we can select the move which gives us the best outcome (guaranteed).

We can see this process in a simplified example using Tic-Tac-Toe. In this scenario, it's best for us to place the X in the bottom left, since it guarentees us a win. It's possible for us to win with the other options as well, but this isn't guaranteed if our opponent also plays perfectly.
Alpha Beta Pruning
The technique of Alpha Beta Pruning builds on top of the Minimax algorithm. This algorithm was developed independently by a number of computer scientists in the 1950s and 60s, and allows us to significantly speed up our evaluation.
The specific steps require some effort to comprehend, but the basic idea is that we can skip (or prune) branches that are guaranteed to not affect the final outcome.
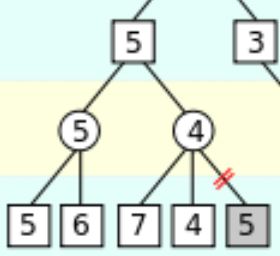
In this example, we start out with only the bottom row given, and everything else is blank. In the first subbranch (with the 5 and 6), we assign the parent node as 5, which is the minimum of 5 and 6. For the second subbranch (with 7, 4, and 5), we take 7 and 4 and get the minimum value as 4. At this point, we can actually the last number in the subbranch (in this case 5), because it is impossible for it to affect the final outcome.
Let's call this last number ![]() . If
. If ![]() , than this doesn't affect the minimum value, because
, than this doesn't affect the minimum value, because ![]() is greater than our current minimum. If
is greater than our current minimum. If ![]() , then our opponent would choose
, then our opponent would choose ![]() on his first move, but this is irrelevant, as we would never choose to go into this branch, we have another branch which guarantees us a higher score.
on his first move, but this is irrelevant, as we would never choose to go into this branch, we have another branch which guarantees us a higher score.
Technically, this algorithm keeps track of all this information using values called ![]() and
and ![]() , but all you need to know about Alpha Beta Pruning is that it provides a significant speedup to our algorithm. Just look at the following example.
, but all you need to know about Alpha Beta Pruning is that it provides a significant speedup to our algorithm. Just look at the following example.

Normally, evaluating this tree would require us to look at ![]() board states, since there are 5 open squares on the initial state. However, by pruning branches that we are never going to check, we have reduced the number of playouts to only 15!
board states, since there are 5 open squares on the initial state. However, by pruning branches that we are never going to check, we have reduced the number of playouts to only 15!
Evaluation
While the above algorithms work great in a small game like Tic-Tac-Toe, it doesn't work as well in chess because the branching factor is so enormous. It's estimated that there are ![]() possible chess games starting from the initial board position, which is far more than a computer could ever keep track of.
possible chess games starting from the initial board position, which is far more than a computer could ever keep track of.
Instead, modern engines work by playing out moves only up to a certain depth (say 20 moves per side), and just evaluating the board state at that position. By cutting off the depth at this level, we evaluate each of these board states and run the Alpha Beta algorithm on this limited tree. The catch is - how do we evaluate a given state?
Let's take a look at Stockfish, the best traditional engine available, which also happens to be open source and extensively documented. Essentially, computer scientists and chess players have come together to come up with an extremely complicated formula involving hundreds of parameters all calculating various aspects of the position.
This can be compared to a naive approach which would just add up all the material that each side has. Yes, Stockfish takes this into account, but there is a lot more granularity that is applied. A pawn might be worth 1 point, but a passed pawn on the 7th might be worth 5 points. The Stockfish evaluation also takes into account more subtle positional factors such as tempo, initiative, space, and mobility. The overall formula is quite complex, but if you're interested, you can take a look at https://hxim.github.io/Stockfish-Evaluation-Guide/.
Conclusion
Believe it or not, this is all it really takes to build a chess engine! Using just the Alpha Beta algorithm and a basic evaluation function, you can write your own engine from scratch! The key aspect that differentiates traditional chess engines (like Stockfish, Fritz, Komodo, etc), is their individual evaluation functions, and any improvements in runtime that they have implemented so that they can evaluate more positions faster and deeper.
In my next few posts, I plan to explore more advanced types of engines involving neural networks, like Alpha Zero and Stockfish NNUE. Stay tuned for my next updates!



2 Comments
A Brief Guide to Neural Network Chess Engines – Saumik Narayanan · January 18, 2021 at 7:14pm
[…] week, I wrote an article explaining the basics on traditional chess engines. Today, I will go over the new generation of […]
A Brief Guide to Stockfish NNUE – Saumik Narayanan · January 26, 2021 at 4:33pm
[…] my last two posts, I gave brief overviews to two of the more established paradigms for chess engines, […]