In my last two posts, I gave brief overviews to two of the more established paradigms for chess engines, represented by Stockfish and AlphaZero. In this post, I will go over the latest engine on the block - Stockfish NNUE. NNUE was integrated into the main Stockfish branch in late 2020 with incredible results!
What is Stockfish NNUE?
Essentially, Stockfish NNUE incorporates the power of neural networks into a traditional chess engine. However, the architecture of Stockfish NNUE is extremely different from the neural networks that Leela or AlphaZero use. Engines of the latter type are extremely deep, convolutional neural networks with as many as 40 layers. Because of this, evaluating positions is quite slow. Even with a strong GPU, AZ calculates around 4 orders of magnitude fewer positions than Stockfish 11 would. Thankfully, this deep convolutional NN is strong enough that analyzing 40 thousand positions is enough to perform as well or even better than the 100 million positions that Stockfish 11 can analyze in a single second.
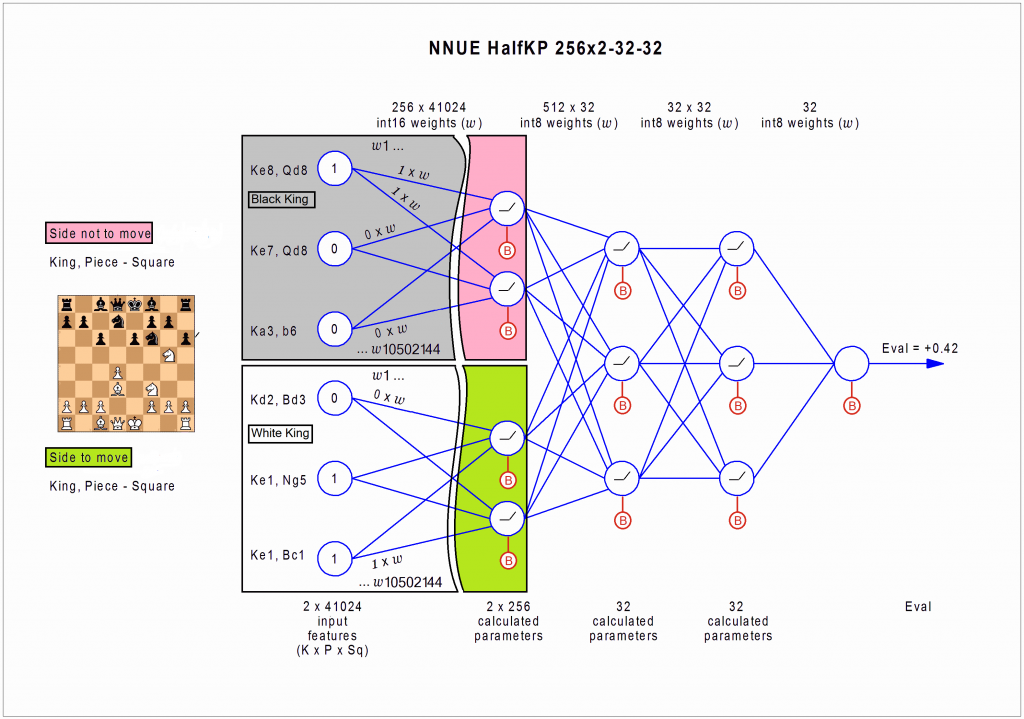
So what is different about NNUE? As it turns out, the network architecture is completely different. Instead of a deep convolutional NN, NNUE uses a shallow, fully connected network, with 4 hidden layers instead of 40.
In addition, NNUE uses an optimization technique that provides an additional speedup. It took me some time to understand how it worked, but once I did, it seems to be extremely elegant. Instead of going over what is actually happening in the network, let me give an analogy.
Let's say we ask a computer to calculate a very multiplication, say 
. This would be a little slow for a computer (relatively of course), but it would duly give us the answer of 
. Now, let's ask the computer to compute 
, which is almost exactly the same as the first calculation, but not quite. A naive computer would start from scratch to do the computation all over again. However, a smarter computer would realize that we've basically solved most of this problem already, and instead of starting from scratch, we can instead calculate 
, or 
. By using our previous answer in the current answer, we've turned a slow multiplication into a very easy addition problem.
NNUE applies essentially this same principle to matrix calculations inside of the neural network. While it might be slow to evaluate a single position using a neural network instead of a traditional evaluation expression, we can use our evaluation from the current position to speed up evaluations of very similar positions (for example positions one move in the future). This allows us to build search trees much much quicker than AlphaZero could. Overall, NNUE can analyze something around 60 million positions per second, closer to SF 11's 100 million positions than Leela's 40 thousand! Because NNUE's architecture is much much smaller than Leela's, the individual sub-evaluations aren't as good as Leela's, but the huge number of positions analyzed allows NNUE to be stronger overall. Also, the small networks mean that NNUE works very well with just a CPU, while A0 or Leela require hefty GPUs to run well.
How is Stockfish NNUE Trained?
Instead of training the engine completely from scratch, NNUE is trained on positions that Stockfish 11 has already analyzed. The position itself, along with SF11's evaluation of the position and search depth is fed into NNUE's model and serves as a supervised ground truth for the model. Thus, NNUE can't be considered a "Zero" engine, since it is still using all the hand-trained parameters to evaluate positions, NNUE just puts these hand-trained features behind a neural network model.
Conclusion
This has been my last guide to how computer chess engines work. Tomorrow, the new semester is starting, and I'll be back to work on classes and doing research full time. See you next week!
2 Comments
Moses · June 24, 2021 at 12:23pm
This is an excellent, really clear description of NNUE. It is really telling when the description of a topic is this straightforward and illuminating – it bespeaks an author who genuinely understands the underlying concepts, and is doing more than simply restating the work of others. I note in particular how easily and intuitively you describe the concept of “efficient updating,” (a concept which many authors have tried and struggled to explain, often by providing a math-y graphical depiction of efficient updating derived from the original Shogi NNUE paper) as well as a perfectly clear and convincing explanation of why stockfish NNUE cannot genuinely be considered a “zero,” or human-evaluation-free, chess engine. kudos.
Random Protist · August 2, 2021 at 8:16am
I agree with Moses comment, it was a very satisfying to read and to see those very effortless analogies and explanations of something so complex.