Rotation 2 Final Report

Introduction

In order to create a surgery schedule for a hospital’s operating rooms, the hospital must predict how long each surgery will take. However, surgery durations are not deterministic, and hospitals must rely on the frequently inaccurate predictions of surgeons, where errors may result in underutilization of staff and resources or overbooking and cancelled surgeries. Prior studies have attempted to use machine learning techniques to provide better predictions for surgery durations, but these studies suffered from several limitations – including small datasets, a subset of procedure types, lack of information about the underlying surgery distribution, and an absence of unstructured input data, such as free-form text.

Jiao et al. published a recent paper, Probabilistic forecasting of surgical case duration using machine learning: model development and validation, which addresses many of these limitations. The dataset contained 53,783 surgical cases performed at the St. Louis Children’s Hospital between April 2013 and December 2017.

The key novelty of this paper was the loss function. Instead of predicting a single output value to represent the model forecast, Jiao’s model predicts a mixture density network (MDN) where the underlying distribution is a sum of multiple log-normal distributions. Jiao then evaluates his prediction distributions using a performance score called continuous ranked probability score (CRPS), an extension of mean absolute error.

Contributions

My goals for this rotation were to extend the work done by Jiao and improve his model. My contributions for the rotation were concentrated in two areas. First, I drastically decreased the amount of time necessary to train and test a model, using methods such as implementing a closed-form solution for CRPS, rewriting the neural network model to take advantage of optimizations in Keras, and taking advantage of multi-core processors. Second, I experimented with ways to improve the structure of the model itself, by adding features such as shared layers and dropout layers, as well as modifying the loss function used during training.

Closed Form Solution for CRPS

CRPS is a scoring measure which allows us to measure the distance between an observation and a distribution. The CRPS measure is denoted by the following equation:

   

, where represents the Cumulative Distribution Function of the distribution. CRPS is an ideal scoring measure for forecasting, as it considers the entire distribution in the score, and rewards both accurate and precise forecasts. For this reason, CRPS is a very common scoring measure in a different domain of forecasting – meteorology. The other reason that CRPS is ideal is it’s measured in the same units as the outcome itself (in this case minutes), compared to other measures such as negative log likelihood (NLL) which creates very unintuitive results. In fact, in the deterministic forecast, CRPS actually collapses down to a more common scoring measure, mean absolute error (MAE). Thanks to this property, CRPS allows us to directly compare results with prior papers which use MAE as a scoring measure.

While CRPS has a number of great properties, a significant downside is that numerically evaluating this integral is extremely slow and is in fact the biggest bottleneck in Jiao’s network. Because calculating CRPS is so slow, there has been some prior work in developing closed-form integral solutions for certain distributions such as the normal distribution (Gneiting et al), the mixture of normal distributions (Grimit et al), and the log-normal distributions (Baran and Lerch).

However, there is no prior work on deriving the closed-form solution for the distribution used in Jiao’s model – a mixture of log-normal distributions. I spent about a week during the rotation attempting to derive my own solution to the mixture of log-normal distributions. I made some progress on the derivation, but I wasn’t able to complete the derivation, as I didn’t know how to evaluate the squared terms in the integrals.

Unable to use the closed-form solution for the mixture distribution, I tried investigating the actual merit of mixture distributions for our use case. I ran an experiment where I trained a model using the same hyperparameters as Jiao’s original model – 4+4 training epochs, 3 layers in the network, and 10 densities in the mixture distribution. The results were a validation error of 18.17 minutes, and a total training time of 2 hours and 5 minutes.

I then repeated the experiment but used my own implementation of the closed-form CRPS for the single log-normal distribution. The results were markedly better: the validation error actually decreased to 18.12 minutes, and a total training time of 9 minutes – a 2700% improvement in training time. Because there didn’t seem to be any benefit to the mixture distributions, and a huge benefit in using just a single distribution, all future work during this rotation used the single log-normal distribution for experiments.

Compiling the CRPS Metric in Keras

In the original model, calculating CRPS on the validation and test datasets was done by iterating over these datasets one example at a time, calculating the prediction from the model of this example, and then calculating the CRPS of this example.

By rewriting the CRPS calculations to use TensorFlow operations, I was able to compile my CRPS function directly into my Keras model. This allowed me to use the method keras.model.evaluate(), and take advantage of built-in Keras optimizations. As a result, the model experienced another huge jump in evaluation speed. For example, one experiment took 15 minutes to run with the old testing model but takes only 44 seconds with the new compiled tester, over a 2000% improvement in runtime.

Python Multi-Core Processing

The last improvement I made to the model runtime was to take advantage of Python’s multiprocessing module to use all 16 cores of the WashU server. This resulted in a performance improvement of about 1200%.

When taking all of these model improvements into account, the updated model can perform over 6500 experiments in the time that the old model would need to run a single experiment.

Shared Model Layers

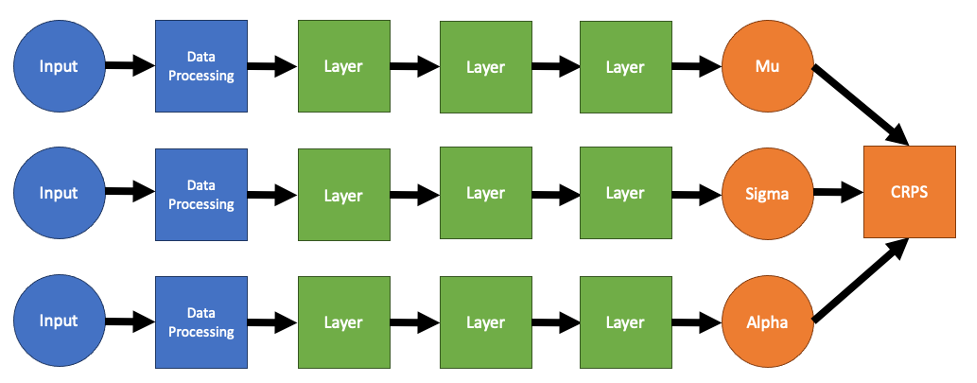
In Jiao’s model, there were three sequences of layers which calculated mu, sigma, and alpha respectively. However, there are several redundancies in this model. Generally, in multi-layer neural networks, the first few layers learn more general features of the input data, and the last layers are aim on learning the output data. As a result, there is no reason to have three separate streams for the input data to flow through, since the first few layers in each of the streams will be roughly the same. Instead, we can combine these layers into a single shared network, and only split the network near the end of the network, giving us a model which looks something like this:

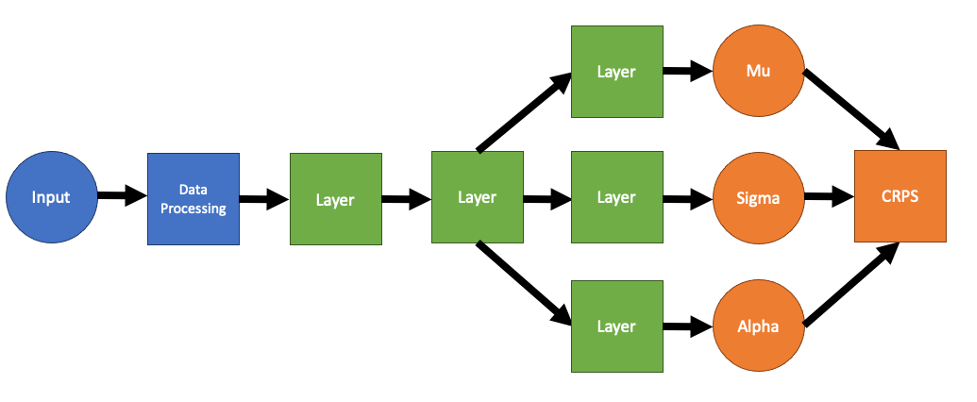
In fact, experiments show that the shared network performs substantially better. The best hyperparameters in the original network have a final validation CRPS and test CRPS of about 17.91 minutes and 18.34 minutes respectively. On the other hand, the best hyperparameters in the shared network have validation and test CRPS values of 17.64 minutes and 18.14 minutes, respectively.

CRPS Loss

In the original model, CRPS is actually too slow to use as the loss function of the neural network. Instead, Jiao’s network uses negative log likelihood as the loss function, since it is also a proper scoring measure but has a much faster computation time than the CRPS integration

Using the closed-form solution though, CRPS becomes a viable alternative loss function to use while training. In fact, using CRPS should result in better performance overall, since we will be using the same loss function in both the training phase and the test phase.

While this sounded true on paper, experiments showed that using CRPS as the training loss function actually resulted in worse results overall – with the best validation and test losses of 17.82 minutes and 18.15 minutes, respectively. The reason why CRPS loss performs worse than NLL loss is currently unknown, more experimentation and analysis is necessary in order to understand the underlying reasons behind this phenomenon.

Dropout Layers

The last set of experiments I performed on the model was on inserting Dropout layers into the model. Dropout layers randomly set values inside of the neural network to zero during training. While this may seem counterintuitive, it has been shown in many domains to improve models overall, by mitigating the risks of overfitting during training. A second effect of dropout is that it introduces probabilistic uncertainty into the model, as the model can’t predict ahead of time which edges in the neural network will be zeroed out.

In order to test whether or not Dropout was beneficial in our network, I added a Keras Dropout layer after each Dense layer in our model. I ran several experiments with different sets of hyperparameters in the model. Unfortunately, I wasn’t able to finish my analysis of Dropout during this rotation as my time ran out. From my preliminary results so far, I found that introducing a dropout level of 40% seemed to slightly improve the validation levels of the model, going from 18.34 minutes and 18.69 minutes to 18.31 minutes and 18.67 minutes for the validation data and test data, respectively.

Future Work

The immediate next steps for this project are to run more experiments on the existing model varieties analyzed and begin to look at a few new model variations as well – for example Bayesian Neural Networks and Transformers over LSTMs.

The next major approach in this project is to start looking at intraoperative data in addition to the preoperative data that we have been analyzing so far. With this data, we could begin to modify and update our forecasts on surgery duration in real-time, providing a much more effective and robust system. In the long term, we would want to integrate the forecasts from this project into actual scheduling programs in use at hospitals.

Conclusion

Overall, I’m quite happy with my progress on the surgery forecasting project during my rotation. I was able to implement several measures which sped up the model by several orders of magnitudes. Additionally, I performed several experiments on the structure of the model. Two of my experiments – dropout and CRPS loss are still inconclusive, while the shared layers model has shown some significant improvement over the previous model.